Построить на плоскости область решений системы линейных неравенств и геометрически найти наименьшее и наибольшее значения
|
ИНФОРМАЦИЯ
|
|
|
Вид работы:
|
Контрольная работа
|
|
Дисциплина:
|
|
|
ВУЗ:
|
|
|
Город, год:
|
2020
|
|
Уникальность:
|
не определен % по системе Антиплагиат
|
Исследование операций и методы оптимальных решений. Контрольная работа, решение 6-ти заданий (задачи линейного и нелинейного программирования, транспортная задача, задачи по теории игр).
Задание 1
Построить на плоскости область решений системы линейных неравенств и геометрически найти наименьшее и наибольшее значения
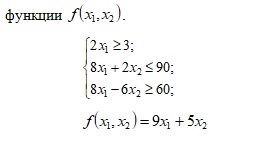
Задание 2
Предприятию необходимо перевезти со склада по железной дороге продукцию трех видов: продукции первого вида не более c1 изделий, продукции второго вида не более c2 изделий и продукции третьего вида не более c3 изделий. Для этой перевозки подразделение железной дороги может выделить специально оборудованные вагоны двух типов A и B. Для полной загрузки вагона в него следует помещать продукцию всех трех видов. При этом в вагон типа A входят a1 изделий первого вида, a2 изделий второго вида и a3 изделий третьего вида. В вагон типа B входят b1 изделий первого вида, b2 изделий второго вида и b3 изделий третьего вида. Экономия от перевозки в вагоне типа A составляет a руб., в вагоне типа B – b руб.
Сколько вагонов каждого типа следует выделить для перевозки, чтобы суммарная экономия от перевозки была наибольшей?
Найти решение двумя способами: геометрически и симплекс методом.

Задание 3
Имеются три пункта поставки однородного груза А1, А2, А3 и пять пунктов В1, В2, В3, В4, В5 потребления этого груза. На пунктах А1, А2 и А3 находится груз в количестве соответственно а1, а2 и а3 т. В пункты В1, В2, В3, В4 и В5 требуется доставить соответственно b1, b2, b3, b4 и b5 т груза. Расстояния между пунктами поставки и пунктами потребления приведены в следующей таблице.

Задание 4
Найти наибольшее и наименьшее значения функции в заданной области графическим методом. Применить метод множителей Лагранжа для поиска наименьшего значения этой функции.
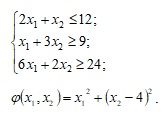
Задание 5
Определить нижнюю и верхнюю цену игры, найти оптимальное решение и цену игры, заданной матрицей 2x2:
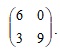
Задание 6
Предприятие может оказывать транспортные услуги трех видов А1, А2, А3, получая при этом прибыль, зависящую от спроса, который может находится в одном из четырех состояний В1, В2, В3, В4.
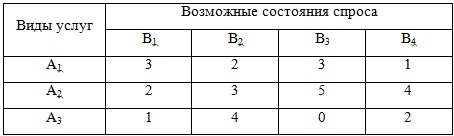 Элементы матрицы характеризуют величину прибыли аij, которую получит предприятие, если будет оказывать i-й вид транспортных услуг при j-м состоянии спроса на эти услуги.
Элементы матрицы характеризуют величину прибыли аij, которую получит предприятие, если будет оказывать i-й вид транспортных услуг при j-м состоянии спроса на эти услуги.Необходимо определить оптимальные пропорции оказываемых предприятием видов услуг, реализация которых обеспечила бы ему максимально возможную выручку независимо от состояния спроса.
|
КУПИТЬ РАБОТУ
|
| СТОИМОСТЬ РАБОТЫ:
|
980 руб.
|
| - Введите нужную сумму и нажмите на кнопку "Перевести"
|
|
| - После оплаты отправьте СКРИНШОТ ОПЛАТЫ и ССЫЛКУ НА РАБОТУ на почту Studgold@mail.ru
|
|
| - После проверки платежа файл будет выслан на вашу почту в течение 48 ЧАСОВ.
|
|
| - Если цена работы не указана или менее 300 руб., то цену необоходимо уточнить в службе поддержки и только потом оплачивать.
|
|
| ПОДДЕРЖКА: |
Studgold@mail.ru
|

Минимальная длина комментария - 50 знаков. комментарии модерируются
|
СМОТРИТЕ ТАКЖЕ
|
Контрольная работа по Методам оптимальных решений Вариант 7 [25-02-2015 13:02]
Задача 1 Предприятию необходимо перевезти со склада по железной дороге продукцию трех видов: продукции первого вида не более 684 изделий, продукции второго вида не более 690 изделий и продукции
Предмет: Методы оптимальных решений
Контрольная работа по Методам оптимальных решений Вариант 22 [06-05-2015 19:16]
Задача 1 Предприятию необходимо перевезти со склада по железной дороге продукцию трех видов: продукции первого вида не более 1 870 изделий, продукции второго вида не более 1 455 изделий и продукции
Предмет: Методы оптимальных решений
Контрольная работа по Методам оптимальных решений (задачи линейного программирования графическим и симплекс-методом, транспортная задача) [07-07-2021 11:21]
Задача 1 Для производства стали определенной марки, в которую должны входить химические элементы А,В,С, можно закупать шихту двух видов I и II. Содержание легирующих элементов в 1 т шихты каждого
Предмет: Методы оптимальных решений
Решение 2-х заданий: ресурсная задача (графический и симплексный методы) + транспортная задача (решение 5-ю методами). [28-06-2021 20:20]
Экономико-математическое моделирование и методы оптимизации. Решение 2-х заданий: ресурсная задача (графический и симплексный методы) + транспортная задача (решение 5-ю методами). Вариант 11 Задание
Предмет: Методы оптимальных решений
Исследование операций и методы оптимальных решений. Решение 2-х заданий (решение в Excel + отчет с описанием решения в Word). [17-07-2021 18:41]
Задание 1 Фирма рекламирует свою продукцию с использованием четырех средств: телевидения, радио, газет и афиш. Из различных рекламных экспериментов, которые проводились в прошлом, известно, что эти
Предмет: Методы оптимальных решений
Исследование операций и методы оптимизации. 3 задания (прямая и двойственная задачи линейного программирования, транспортная задача). [26-06-2021 10:05]
Исследование операций и методы оптимизации. Контрольная работа, 3 задания (прямая и двойственная задачи линейного программирования, транспортная задача). Задача 1 Для изготовления двух видов
Предмет: Методы оптимальных решений

