Контрольная работа по Методам оптимальных решений Вариант 6
|
ИНФОРМАЦИЯ
|
|
|
Вид работы:
|
Контрольная работа
|
|
Дисциплина:
|
|
|
ВУЗ:
|
|
|
Город, год:
|
Тула 2015
|
|
Уникальность:
|
% по системе
|
Задача 1.
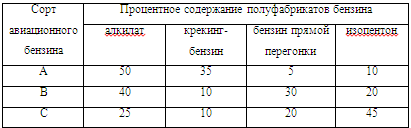
Нефтеперерабатывающий завод получает четыре полуфабриката: 100 тыс.л. алкилата, 80 тыс.л. крекинг-бензина, 60 тыс.л. бензина прямой перегонки, 100 тыс.л. изопентона. В результате смешивания этих четырех компонентов в разных пропорциях образуются три сорта авиационного бензина: бензин А, бензин В, бензин С. Процентное содержание полуфабрикатов для каждого сорта бензина приведено в таблице. Стоимость 1 тыс.л. указанных сортов бензина равна 120 д.е., 100 д.е., 150 д.е.
Составьте план выпуска разных сортов авиационного бензина из условия максимальной стоимости всей продукции.
Задача 2.
Имеются три элеватора, в которых сосредоточено соответственно 4200, 1200 и 3000 т зерна. Зерно необходимо перевезти пяти хлебозаводам в количестве 1500, 2500, 1600, 1400 и 1400 т каждому. Значения стоимости перевозки 1 т зерна от элеваторов до хлебозаводов указаны в таблице:
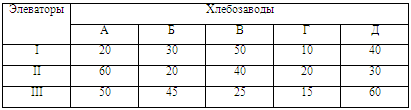
Спланируйте перевозки зерна на условия минимизации транспортных расходов.
Задача 3.
Финансовый аналитик фирмы «АВС» консультирует клиента по оптимальному инвестиционному портфелю. Клиент хочет вложить средства (не более 25 000 долл.) в два наименования акций крупных предприятий в составе холдинга «Дикси». Анализируются акции «Дикси-Е» и «Дикси-В». Цены на акции: «Дикси-Е» – 5 долл., «Дикси-В» – 3 долл. за акцию. Клиент уточнил, что он хочет приобрести максимум 6000 акций обоих наименований, но при этом акций одного вида должно быть не более 5000 штук.
По оценкам аналитика, прибыль от инвестиций в следующем году составит: по акции «Дикси-Е» – 1,1 долл., по акции «Дикси-В» – 0,9 долл.
Дайте рекомендации клиенту по оптимизации прибыли от инвестиций.
Постройте экономико-математическую модель задачи, дайте необходимые комментарии к ее элементам и получите решение графическим методом. Что произойдет, если решать задачу на минимум, и почему?
Задача 4.
Предприятие пищевой промышленности ежемесячно использует около 25000 стеклянных банок объемом 1 л для производства фруктового сока. Месячная стоимость хранения одной банки – 10 коп. Компания работает в среднем 20 дней в месяц. Затраты на размещение заказа составляют 300 руб. Доставка осуществляется в течение одного дня.
Определите:
а) оптимальный объём заказа;
б) годовые расходы на хранение запасов;
в) период поставок;
г) точку заказа.
Задача 5.
В бухгалтерии организации в определенные дни непосредственно с сотрудниками работают два бухгалтера. Если сотрудник заходит в бухгалтерию для оформления документов (доверенностей, авансовых отчетов и пр.) в тот момент, когда оба бухгалтера заняты обслуживанием ранее обратившихся коллег, то он уходит из бухгалтерии, не ожидая обслуживания. Статистический анализ показал, что среднее число сотрудников, обращающихся в бухгалтерию в течение часа, равно λ, а среднее время, которое затрачивает бухгалтер на оформление документа, - Тср мин.
Оцените основные характеристики работы данной бухгалтерии как СМО с отказами (указание руководства не допускать непроизводительных потерь рабочего времени!). Определите, сколько бухгалтеров должно работать в бухгалтерии в отведенные дни с сотрудниками, чтобы вероятность обслуживания сотрудников была выше 85%.
У к а з а н и е. Для исследования предлагаемой хозяйственной ситуации используйте методы теории массового обслуживания. При моделировании предполагается, что поток требований на обслуживание является простейшим (пуассоновским), а продолжительность обслуживания распределена по экспоненциальному (показательному) закону.
Задачу решите с помощью средств MS Excel.
λ = 12 , Тср = 1/ μ = 10.
Задача 6.
Статистический анализ показал, что случайная величина Х (длительность обслуживания клиента в парикмахерской) следует показательному закону распределения с параметром μ, а число клиентов, поступающих в единицу времени (случайная величина Y), - закону Пуассона с параметром λ.
Организуйте датчики псевдослучайных чисел для целей статистического моделирования (использование метода Монте-Карло).
Значения параметров: μ = 0,8, λ = 2,1.
|
КУПИТЬ РАБОТУ
|
| СТОИМОСТЬ РАБОТЫ:
|
|
| - Введите нужную сумму и нажмите на кнопку "Перевести"
|
|
| - После оплаты отправьте СКРИНШОТ ОПЛАТЫ и ССЫЛКУ НА РАБОТУ на почту Studgold@mail.ru
|
|
| - После проверки платежа файл будет выслан на вашу почту в течение 48 ЧАСОВ.
|
|
| - Если цена работы не указана или менее 300 руб., то цену необоходимо уточнить в службе поддержки и только потом оплачивать.
|
|
| ПОДДЕРЖКА: |
Studgold@mail.ru
|

Минимальная длина комментария - 50 знаков. комментарии модерируются
|
СМОТРИТЕ ТАКЖЕ
|
Модели и методы принятия решений. Контрольная работа, решение 3-х заданий (задача линейного программирования, транспортная задача, задача о межотраслевом балансе) [20-07-2021 16:47]
Задания №1 и №2 решены в Excel с помощью поиска решений + отчет с описанием решения в Word. Задание №3 решено в Word. Задание 1 Решить задачу оптимизации - построить математическую модель задачи
Предмет: Методы оптимальных решений
Разработка управленческих решений. Решение 2-х задач: 1) Для приготовления комбикорма совхоз может закупить зерно...; 2) Трем деревообрабатывающим фабрикам поставляется лесоматериал... [05-08-2021 18:15]
Задание 1 По содержательной постановке задачи необходимо построить математическую оптимизационную модель и графическим способом найти её решение. Для приготовления комбикорма совхоз может закупить
Предмет: Методы оптимальных решений
Задачи по Методам оптимальных решений. Решение 2-х заданий: задача линейного программирования (графический и симплексный методы, двойственная задача, интервалы устойчивости...) и транспортная задача [27-07-2021 16:05]
Задача 1 Решить задачу линейного программирования. Предприятие выпускает два вида продукции I и II, для производства которых используется сырье трех видов. На изготовление единицы изделия I требуется
Предмет: Методы оптимальных решений
Контрольная работа №2 по Методам оптимальных решений Вариант 30 [12-08-2015 02:32]
Задача 1. Имеется три завода А1, А2, А3 объем производства, которых соответственно равен а1, а2, а3 тонн в сутки. Эти заводы ежедневно удовлетворяют потребности четырех строительных объектов В1, В2,
Предмет: Методы оптимальных решений
Контрольная работа №2 по Методам оптимальных решений Вариант 27 [20-08-2015 11:01]
Задача 1 Имеется три завода А1, А2, А3 объем производства, которых соответственно равен а1, а2, а3 тонн в сутки. Эти заводы ежедневно удовлетворяют потребности четырех строительных объектов В1, В2,
Предмет: Методы оптимальных решений
Задачи линейного программирования и транспортные задачи. Решение 4-х задач. Решение в Excel + отчет с описанием решения в Word. [03-07-2021 09:29]
Линейное программирование Задача 1 Составить питательную смесь из двух видов продуктов В1, В2, причем в смеси должно быть не менее заданных величин содержания питательных веществ А1,А2,А3. Задана
Предмет: Методы оптимальных решений

