Контрольная работа №2 по Методам оптимальных решений Вариант 27

Задача 1

Имеется три завода А1, А2, А3 объем производства, которых соответственно равен а1, а2, а3 тонн в сутки. Эти заводы ежедневно удовлетворяют потребности четырех строительных объектов В1, В2, В3, В4 в количествах b1, b2, b3, b4 тонн в сутки соответственно. Стоимость (тыс. руб.) перевозки единицы продукции с каждого завода на каждый строительный объект задана матрицей тарифов С=(сij), i=1,2,3,4, j=1,2,3. Исходные данные задачи приведены в таблице:

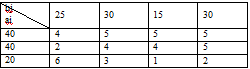
Найти такой план транспортировки груза, чтобы общие затраты на перевозки грузов были минимальными.

Задача 2

Даны производственная функция Кобба-Дугласа Q( K, L) = 4K4/5L1/5 и цены на ресурсы рK =8, pL =2. С помощью теоремы Куна-Таккера найдите объемы ресурсов K и L , при которых затраты на производство не менее 192 единиц продукции минимальны.

Задача 3

Имеются четыре предприятия, между которыми необходимо распределить 100 тыс. усл. ед. средств. Значения прироста выпуска продукции на предприятиях в зависимости от выделенных средств Х представлены в таблице.

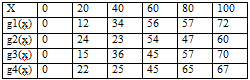
Составить оптимальный план распределения средств, позволяющий максимизировать общий прирост выпуска продукции.

Задача 4

Последовательность работ при разработке и внедрении задачи (программного комплекса) в АСУ приведена в таблице 

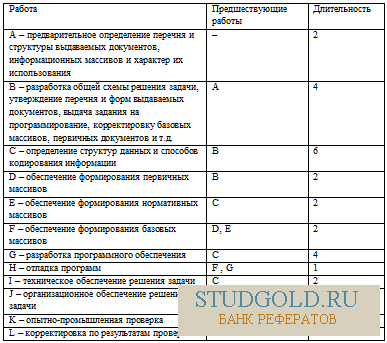
Построить сетевой график. Определить критические пути и их длину. Результаты решения задачи планирования отобразить в виде календарного плана. 

Задача 5

Предприятие может выпускать 3 вида продукции А1, А2 и А3, получая при этом прибыль, зависящую от спроса, который может быть в одном из 4-х состояний (В1, В2, В3, В4). Элементы платежной матрицы характеризуют прибыль, которую получат при выпуске i-й продукции при j-м состоянии спроса. Игра предприятия А против спроса В задана платежной матрицей:

Определить оптимальные пропорции в выпускаемой продукции, гарантирующие максимизацию средней величины прибыли при любом состоянии спроса, считая его определенным. Задача сводится к игровой модели.