Контрольная работа №2 по Методам оптимальных решений Вариант 30

Задача 1. Имеется три завода А1, А2, А3 объем производства, которых соответственно равен а1, а2, а3 тонн в сутки. Эти заводы ежедневно удовлетворяют потребности четырех строительных объектов В1, В2, В3, В4 в количествах b1, b2, b3, b4 тонн в сутки соответственно. Стоимость (тыс. руб) перевозки единицы продукции с каждого завода на каждый строительный объект задана матрицей тарифов С=(сij), i=1,2,3,4, j=1,2,3. Исходные данные задачи приведены в таблице:

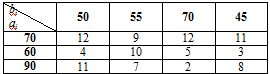
Найти такой план транспортировки груза, чтобы общие затраты на перевозки грузов были минимальными.

Задача 2. Даны производственная функция Кобба-Дугласа Q( K, L) = 2K2/3L1/3 и цены на ресурсы рK=2, pL=8. С помощью теоремы Куна-Таккера найдите объемы ресурсов K и L , при которых затраты на производство не менее 264 единиц продукции минимальны.

Задача 3. Имеются четыре предприятия, между которыми необходимо распределить 100 тыс. усл. ед. средств. Значения прироста выпуска продукции на предприятиях в зависимости от выделенных средств Х представлены в таблице.

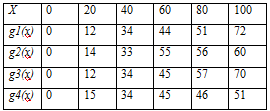
Составить оптимальный план распределения средств, позволяющий максимизировать общий прирост выпуска продукции.

Задача 4. В таблице приведены работы, выполняемые при строительстве нового каркасного дома.

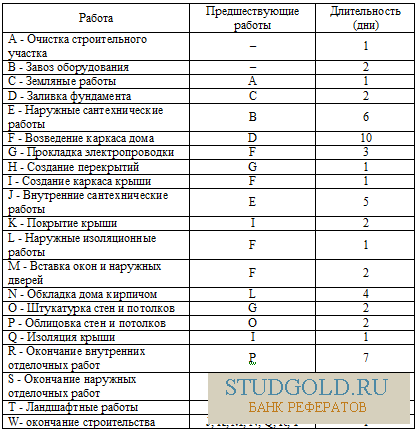
Построить сетевой график. Определить критические пути и их длину. Результаты решения задачи планирования отобразить в виде календарного плана.

Задача 5. Предприятие может выпускать 3 вида продукции А1, А2 и А3, получая при этом прибыль, зависящую от спроса, который может быть в одном из 4-х состояний (В1, В2, В3, В4). Элементы платежной матрицы характеризуют прибыль, которую получат при выпуске i-й продукции при j-м состоянии спроса. Игра предприятия А против спроса В задана платежной матрицей:

Определить оптимальные пропорции в выпускаемой продукции, гарантирующие максимизацию средней величины прибыли при любом состоянии спроса, считая его определенным.