Контрольная работа по Теории вероятности и математической статистике Вариант 3

ИНФОРМАЦИЯ
Вид работы:	Контрольная работа
Дисциплина:	Теория вероятностей и математическая статистика
ВУЗ:	Финансовый университет при правительстве РФ (ВЗФЭИ)
Город, год:	2015
Уникальность:	% по системе

ПОВЫСИТЬ УНИКАЛЬНОСТЬ ТЕКСТА

ПОМОЩЬ В НАПИСАНИИ РАБОТЫ

Контрольная работа № 1

Задача 1. Среди 20 электролампочек 3 нестандартные. Одновременно берут 3 лампочки. Найти вероятность того, что не менее двух лампочек будут стандартными.

Задача 2. В цепи из четырех последовательно соединенных элементов произошло замыкание. Мастер проверяет элементы последовательно, пока не обнаружит замыкание (проверенный элемент повторно не проверяется).

Составить закон распределения числа проверенных мастером элементов.

Найти математическое ожидание, дисперсию и функцию распределения данной случайной величины.

Задача 3. Вероятность выпуска бракованной микросхемы равна 0,002. Какова вероятность того, что из 2000 присланных в магазин микросхем окажется не менее 3 бракованных?

Задача 4. Случайная величина E имеет нормальный закон распределения с параметрами а и б2.

Найти:

а) параметр б2, если известно, что математическое ожидание МЕ=5 и вероятность Р(2-У-8)=0,9973;

б) вероятность Р(Е-0).

Контрольная работа № 2

Задача 1. В некотором городе по схеме собственно - случайной бесповторной выборки было обследовано 80 магазинов розничной торговли из 2500 с целью изучения объема розничного товарооборота. Получены следующие данные.

а) вероятность того, что средний объем розничного товарооборота во всех магазинах города отличается от среднего объема розничного товарооборота, полученного в выборке, не более чем на 4 у.е. (по абсолютной величине);

б) границы, в которых с вероятностью 0,98 заключена доля магазинов с объемом розничного товарооборота от 60 до 90 у.е.;

в) объем бесповторной выборки, при котором те же границы для среднего объема розничного товарооборота (см. п. а) можно гарантировать с вероятностью 0,95.

Задача 2. По данным задачи 1, используя χ2 - критерий Пирсона, на уровне значимости α = 0,05 проверить гипотезу о том, что случайная величина Х – объем розничного товарооборота – распределена по нормальному закону.

Построить на одном чертеже гистограмму эмпирического распределения и соответствующую нормальную кривую.

3. Имеются следующие выборочные данные о рыночной стоимости квартир (тыс. у.е.) и их общей площади (кв. м.)

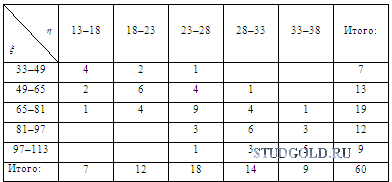
Необходимо:

1. Вычислить групповые средние и , и построить эмпирические линии регрессии.

2. Предполагая, что между переменными и существует линейная корреляционная зависимость:

а) найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать экономическую интерпретацию полученных уравнений;

б) вычислить коэффициент корреляции; на уровне значимости

α = 0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными и ;

в) используя соответствующее уравнение регрессии, оценить стоимость квартиры общей площадью 75 кв. м.

КУПИТЬ РАБОТУ

СТОИМОСТЬ РАБОТЫ:
- Введите нужную сумму и нажмите на кнопку "Перевести"
- После оплаты отправьте СКРИНШОТ ОПЛАТЫ и ССЫЛКУ НА РАБОТУ на почту Studgold@mail.ru
- После проверки платежа файл будет выслан на вашу почту в течение 24 ЧАСОВ.
- Если цена работы не указана или менее 100 руб., то цену необоходимо уточнить в службе поддержки и только потом оплачивать.
ПОДДЕРЖКА:	Studgold@mail.ru

Контрольная работа по Теории вероятности и математической статистике Вариант 3

Комментарии

Минимальная длина комментария - 50 знаков. комментарии модерируются

Контрольная работа № 1 Задача 1. На полке стоят одинаковые по внешнему виду книги: 2 по математике и 3 по физике. Студент последовательно просматривает книги до тех пор, пока не найдет книгу по