Лабораторная работа по Методам оптимальных решений на тему Симплексный метод решения задач линейного программирования

Лабораторная работа, решение 2-х заданий (решение в Word симплексным методом + решение в Excel с помощью поиска решений задания №1)

Тема: «Симплексный метод решения задач линейного программирования»

Задание:

1. Составить экономико-математическую модель задачи.

2. Решить задачу симплексным методом с естественным базисом.

3. Задачу №1 решить в Excel «Поиск решения».

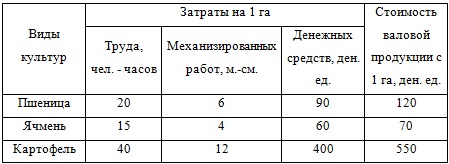
Определить оптимальную структуру посевных площадей, обеспечивающую максимальную прибыль. Хозяйство имеет 4000 га пашни, трудовые ресурсы составляют 80000 чел. – часов, механизированные ресурсы – 30000 м. – см.

Условные данные приведены ниже:

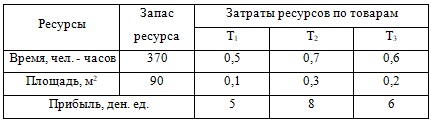
Торговое предприятие реализует товары Т1, Т2 и Т3, используя при этом площади товарных залов и время обслуживающего персонала. Затраты указанных ресурсов на продажу одной партии товара каждого вида, их объемы и прибыль, получаемая от реализации каждой партии товара, приведены в таблице 2. Найти оптимальную структуру товарооборота, обеспечивающую предприятию максимальную прибыль.