Решение 3-х заданий (линейное программирование, матричные игры, сетевое планирование)

ИНФОРМАЦИЯ
Вид работы:	Контрольная работа
Дисциплина:	Методы оптимальных решений
ВУЗ:
Город, год:	2020
Уникальность:	не определен % по системе Антиплагиат

ПОВЫСИТЬ УНИКАЛЬНОСТЬ ТЕКСТА

ПОМОЩЬ В НАПИСАНИИ РАБОТЫ

Работа выполнена в 2020 году. Объем работы – 30 стр. Оформление в Word. Шрифт – 14, интервал – 1,5.
Работа сделана с подробными пояснениями к решению.

Задание 1
Применение методов линейного программирования.

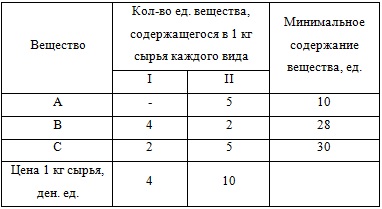
Из двух видов сырья необходимо составить смесь, в состав которой должно входить не менее указанных единиц химического вещества А, В и С соответственно. Цена 1 кг сырья каждого вида, а также количество единиц химического вещества, содержащегося в 1 кг сырья каждого вида, указаны в таблице. Составить смесь, имеющую минимальную стоимость.
Требуется:
1) построить математическую модель задачи;
2) выбрать метод решения и привести задачу к канонической форме;
3) решить задачу (двойственным симплекс-методом);
4) дать геометрическую интерпретацию решения;
5) проанализировать результаты решения.

Задание 2
Методы решения матричных игр.

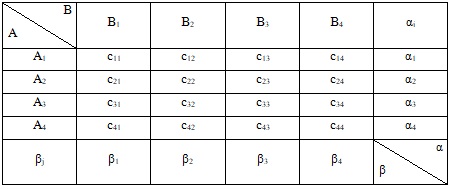
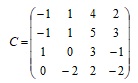
Отрасли А и В осуществляют капитальные вложения в четыре объекта. С учетом особенностей вкладов и местных условий прибыль отрасли А в зависимости от объема финансирования выражается элементами матрицы С. Для упрощения задачи принять, что убыток отрасли В равен прибыли отрасли А. Найти оптимальные стратегии отраслей.
Требуется:
1) свести исходные данные в таблицу и найти решение матричной игры в чистых стратегиях, если оно существует (в противном случае см. следующий п. 2);
2) упростить платежную матрицу;
3) составить пару взаимно двойственных задач, эквивалентную данной матричной игре;
4) найти оптимальное решение прямой задачи (для отрасли В) симплекс-методом;
5) используя соответствие переменных, выписать оптимальное решение двойственной задачи (для отрасли А);
6) дать геометрическую интерпретацию этого решения (для отрасли А);
7) используя соотношение между оптимальными решениями пары двойственных задач, оптимальными стратегиями и ценой игры, найти решение игры в смешанных стратегиях;
8) дать рекомендации по каждой отрасли.

Задание 3
Сетевое планирование.

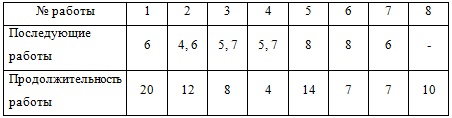
Информация о строительстве комплекса задана нумерацией работ, их продолжительностью (в ед. времени), последовательностью выполнения и оформлена в виде таблицы. За какое минимальное время может быть завершен весь комплекс работ?
Требуется:
1) по данным таблицы построить сетевой график комплекса работ и найти правильную нумерацию его вершин;
2) рассчитать на сетевом графике ранние и поздние сроки наступления событий, а также резервы времени событий;
3) выделить на сетевом графике критические пути;
4) для некритических работ найдем полные и свободные резервы времени;
5) выполнить анализ сетевого графика.


Как повлияет на срок выполнения комплекса работ увеличение продолжительности работы № 3 на 8 месяцев, работы № 7 на 2 месяца? На какое время можно увеличить продолжительность работ № 1 и № 3, не изменяя ранние сроки выполнения последующих работ?

КУПИТЬ РАБОТУ

СТОИМОСТЬ РАБОТЫ:	600 руб.
- Введите нужную сумму и нажмите на кнопку "Перевести"
- После оплаты отправьте СКРИНШОТ ОПЛАТЫ и ССЫЛКУ НА РАБОТУ на почту Studgold@mail.ru
- После проверки платежа файл будет выслан на вашу почту в течение 24 ЧАСОВ.
- Если цена работы не указана или менее 100 руб., то цену необоходимо уточнить в службе поддержки и только потом оплачивать.
ПОДДЕРЖКА:	Studgold@mail.ru