Методы оптимальных решений и математическое моделирование. Решение 3-х заданий (метод множителей Лагранжа, задача о распределении инвестиций, определение производственной функции).
|
ИНФОРМАЦИЯ
|
|
|
Вид работы:
|
Контрольная работа
|
|
Дисциплина:
|
|
|
ВУЗ:
|
|
|
Город, год:
|
2020
|
|
Уникальность:
|
не определен % по системе Антиплагиат
|
Ситуация 1
Определить методом множителей Лагранжа условные экстремумы
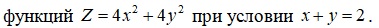
Ситуация 2
Распределить Т=100 тыс .ден.ед. по четырем предприятиям с целью получения максимальной суммарной прибыли. Значения прироста продукции в зависимости от вложенных средств заданы таблицей.
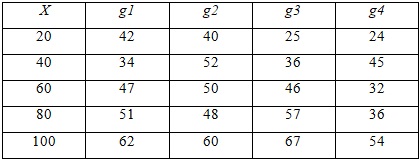
Ситуация 3
Рассмотрим некоторое производство, которое описывается с помощью функции ПФКД. Основные фонды оцениваются в х1 руб., численность работников составляет х2 человек. Средняя производительность труда z=y/х2 руб. Известно также, что для увеличения выпуска продукции на dy требуется увеличить стоимость фондов на dх1 или численность работников на dх2.
Требуется построить для данного предприятия производственную функцию, определив коэффициенты эластичности.
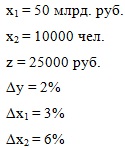
|
КУПИТЬ РАБОТУ
|
| СТОИМОСТЬ РАБОТЫ:
|
450 руб.
|
| - Введите нужную сумму и нажмите на кнопку "Перевести"
|
|
| - После оплаты отправьте СКРИНШОТ ОПЛАТЫ и ССЫЛКУ НА РАБОТУ на почту Studgold@mail.ru
|
|
| - После проверки платежа файл будет выслан на вашу почту в течение 48 ЧАСОВ.
|
|
| - Если цена работы не указана или менее 300 руб., то цену необоходимо уточнить в службе поддержки и только потом оплачивать.
|
|
| ПОДДЕРЖКА: |
Studgold@mail.ru
|

Минимальная длина комментария - 50 знаков. комментарии модерируются
|
СМОТРИТЕ ТАКЖЕ
|
Решение 3-х заданий: нахождение глобальных экстремумов функции (графический метод), использование метода Лагранжа, задача о распределении инвестиций [17-07-2021 19:27]
Методы оптимизации и оптимальных решений. Решение 3-х заданий: нахождение глобальных экстремумов функции (графический метод), использование метода Лагранжа, задача о распределении инвестиций Задание
Предмет: Методы оптимальных решений
Задачи нелинейного программирования (решение графическим методом и методом множителей Лагранжа) и задачи динамического программирования. Контрольная работа, решение 4-х задач. [07-07-2021 18:52]
Задание 1 Решить графическим методом задачу нелинейного программирования. Задание 2 Найти условные экстремумы функции, используя метод множителей Лагранжа. Задание 3 В транспортной сети имеется
Предмет: Методы оптимальных решений
Контрольная работа, решение 3-х заданий (задача нелинейного программирования, задача распределения инвестиций, принятие решений в условиях неопределенности) [18-07-2021 17:26]
Задание 1 1)Составить математическую модель задачи нелинейного программирования 2)Найти решение методом Лагранжа 3)Описать полученные результаты. Предприятие производит металлорежущие станки двумя
Предмет: Методы оптимальных решений
Методы оптимальных решений (вариант 3, АлтИЭ) [27-01-2022 23:48]
Введение3 1 Классическая задача оптимизации, решение методом множителей Лагранжа4 2. Метод динамического программирования6 Заключение10 Список используемых источников11 Сделана в январе 2019 года.
Предмет: Методы оптимальных решений
Построить на плоскости область решений системы линейных неравенств и геометрически найти наименьшее и наибольшее значения [05-07-2021 22:34]
Исследование операций и методы оптимальных решений. Контрольная работа, решение 6-ти заданий (задачи линейного и нелинейного программирования, транспортная задача, задачи по теории игр). Задание 1
Предмет: Методы оптимальных решений
Контрольная работа №1 по Методам оптимальных решений Вариант 30 [13-08-2015 02:30]
Задача. Для изготовления трех видов продукции (A, B, C) используется три вида ресурсов (1, 2, 3). Объем ресурса bi , ( i = 1, 2, 3) нормы его расхода aijна единицу продукции и цена сj, (j
Предмет: Методы оптимальных решений

