Контрольная работа по Теории вероятности и математической статистике Вариант 8
|
ИНФОРМАЦИЯ
|
|
|
Вид работы:
|
Контрольная работа
|
|
Дисциплина:
|
|
|
ВУЗ:
|
|
|
Город, год:
|
Город не указан 2016
|
|
Уникальность:
|
% по системе
|
Задача №1.2
Подбрасываются две игральные кости. Определить вероятность того, что сумма выпавших чисел делится без остатка на шесть.
Задача № 2.30
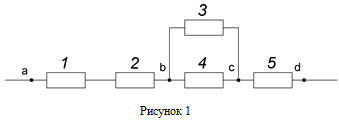
Дана схема соединения элементов, образующих цепь с одним входом и одним выходом (рисунок 1). Предполагается, что отказы элементов являются независимыми в совокупности событиями. Отказ любого из элементов приводит к прерыванию сигнала в той ветви цепи, где находится данный элемент. Вероятности отказа элементов 1, 2, 3, 4, 5 соответственно равны q1=0,1; q2=0,2; q3=0,3; q4=0,4; q5=0,5. Найти вероятность того, что сигнал пройдет со входа на выход.
Задача №3.27
Имеются три одинаковых по виду ящика. В первом ящике 20 белых шаров, во втором - 10 белых и 10 черных шаров, в третьем - 20 черных шаров. Из каждого ящика вынули шар. Затем из этих трех шаров наугад взяли один шар. Вычислить вероятность того, что шар белый.
Задача №4.1
Вероятность изготовления стандартного изделия равна 0,95. Какова вероятность того, что среди десяти изделий не более одного нестандартного?
Задача № 5.28
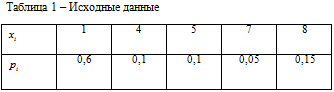
Дискретная случайная величина Х может принимать одно из пяти фиксированных значений x1, x2, x3, x4, x5 с вероятностями p1, p2, p3, p4, p5 соответственно. Вычислить математическое ожидание и дисперсию величины Х. Рассчитать и построить график функции распределения.
Задача № 6.12
Случайная величина Х задана плотностью вероятности:
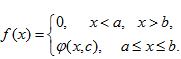
Определить константу С, математическое ожидание, дисперсию, функцию распределения величины Х, а также вероятность ее попадания в интервал .
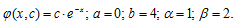
Задача № 7.23
Случайная величина Х распределена равномерно на интервале [a,b]. Построить график случайной величины Y=(X) и определить плотность вероятности g(y).
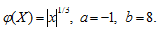
Задача № 8.15
Двухмерный случайный вектор (Х, У) равномерно распределен внутри выделенной жирными прямыми линиями на рисунок 4 области B. Двухмерная плотность вероятности f(x,y) одинакова для любой точки этой области B:
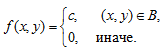
Вычислить коэффициент корреляции между величинами X и Y.

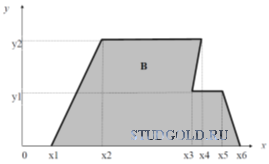
Задача № 9
По выборке одномерной случайной величины:
- получить вариационный ряд;
- построить график эмпирической функции распределения F*(x);
- построить гистограмму равноинтервальным способом;
- построить гистограмму равновероятностным способом;
- вычислить точечные оценки математического ожидания и дисперсии;
- вычислить интервальные оценки математического ожидания и дисперсии (γ = 0,95);
- выдвинуть гипотезу о законе распределения случайной величины и проверить ее при помощи критерия согласия 2 и критерия Колмогорова ( = 0,05).
Одномерная выборка:
Размер выборки
1,321,433,010,500,440,290,530,830,790,951,500,931,041,150,54
0,141,470,590,021,161,070,020,490,040,280,590,170,620,713,16
1,880,832,311,950,071,411,870,931,751,931,921,990,411,000,19
0,131,842,110,540,530,500,274,320,780,171,062,240,150,470,25
1,310,200,550,170,170,620,001,040,601,410,592,900,100,683,97
0,660,762,510,750,011,630,310,701,372,830,532,460,870,912,70
0,220,080,771,861,180,052,482,640,680,02
Задача №10
По выборке двухмерной случайной величины:
- вычислить точечную оценку коэффициента корреляции;
- вычислить интервальную оценку коэффициента корреляции ;
- проверить гипотезу об отсутствии корреляционной зависимости ;
- вычислить оценки параметров a0 и a1 линии регрессии ;
- построить диаграмму рассеивания и линию регрессии.
Выборка:
( 4.77; 1.47) ( 1.77; 3.86) ( 5.30; 8.30) ( 0.25; 4.09) ( -2.78; 0.55) ( 3.61; 8.59) ( 1.48; 5.84) ( 1.58; 4.76)
( 8.01; 5.71) ( 4.23; 7.36) ( 9.80; 15.22) ( 4.01; 4.68) ( 2.22; 4.70) ( 0.23; 9.23) ( 6.81; 7.64) ( 0.70; 1.12)
( 5.76; 12.74) ( -4.64; -0.27) ( 2.41; 6.13) ( 3.22; 6.77) ( 5.68; 12.31) ( 2.05; 6.32) ( 4.03; 1.89) ( 8.78; 8.93)
( 5.30; 5.94) ( 5.35; 10.72) ( 4.05; 9.71) ( 6.55; 11.21) ( 9.43; 7.51) ( 6.88; 4.32) ( 3.96; 7.38) ( 0.18; 2.54)
( 3.31; 5.78) ( 5.51; 4.20) ( 11.42; 6.69) ( 3.87; 5.42) ( 4.93; 8.14) ( 7.13; 7.49) ( 4.68; 4.21) ( 5.62; 9.29)
( -1.35; 0.90) ( 0.16; 7.25) ( 6.28; 3.53) ( 9.93; 11.77) ( 5.62; 0.80) ( -2.01; 2.12) ( 0.44; 3.62) ( 5.97; 6.68)
( 9.27; 8.18) ( 1.55; 4.77)
|
КУПИТЬ РАБОТУ
|
| СТОИМОСТЬ РАБОТЫ:
|
|
| - Введите нужную сумму и нажмите на кнопку "Перевести"
|
|
| - После оплаты отправьте СКРИНШОТ ОПЛАТЫ и ССЫЛКУ НА РАБОТУ на почту Studgold@mail.ru
|
|
| - После проверки платежа файл будет выслан на вашу почту в течение 48 ЧАСОВ.
|
|
| - Если цена работы не указана или менее 300 руб., то цену необоходимо уточнить в службе поддержки и только потом оплачивать.
|
|
| ПОДДЕРЖКА: |
Studgold@mail.ru
|

Минимальная длина комментария - 50 знаков. комментарии модерируются
|
СМОТРИТЕ ТАКЖЕ
|
Случайные события (Вариант 5) [27-06-2017 13:24]
1.Из таблицы случайных чисел наудачу взято одно число. Событие А – выбранное число делится на 2; Событие В—выбранное число делится на 3. Что означают события А+В, А•В, A, B? 2.В лотерее 1000 билетов,
Предмет: Теория вероятностей и математическая статистика
Контрольная работа №3 по Теории вероятностей и математической статистике Вариант 8 Методичка 2010 [18-09-2014 11:48]
1. В двух ящиках находится по 16 деталей. Причем в первом ящике находится 9 стандартных деталей, а во втором – 12. Из первого ящика наугад извлекли одну деталь и переложили во второй ящик. Найти
Предмет: Теория вероятностей и математическая статистика
Контрольная работа №3 по Теории вероятностей и математической статистике Вариант 8 [14-03-2011 14:28]
1. В двух ящиках находится по 16 деталей. Причем в первом ящике находится 9 стандартных деталей, а во втором – 12. Из первого ящика наугад извлекли одну деталь и переложили во второй ящик. Найти
Предмет: Теория вероятностей и математическая статистика
Контрольная работа №3 по Теории вероятностей и математической статистике Вариант 8 Методичка 2010 [11-10-2014 17:00]
Контрольная работа №3 1. В двух ящиках находится по 16 деталей. Причем в первом ящике находится 9 стандартных деталей, а во втором – 12. Из первого ящика наугад извлекли одну деталь и переложили во
Предмет: Теория вероятностей и математическая статистика
Контрольная работа по Теории вероятностей и математической статистике Вариант 9 [05-05-2015 13:30]
Задача 1. Из трех бухгалтеров, восьми менеджеров и шести научных работников необходимо сформировать комитет из 10 человек. Найти вероятность того, что в комитете окажутся: один бухгалтер, пять
Предмет: Теория вероятностей и математическая статистика
Контрольная работа по Теории вероятностей и математической статистике Вариант 9 [11-03-2011 10:28]
1. В поселке имеется 6 производственных предприятий, 8 магазинов и 4 банка. Вероятность того, что имеется свободная вакансия бухгалтера равна: 0,4 для предприятия; 0,3 для магазина; 0.6 для банка. 1)
Предмет: Теория вероятностей и математическая статистика

