Теория игр и принятия решений. Контрольная работа, решение 7-ми заданий
|
ИНФОРМАЦИЯ
|
|
|
Вид работы:
|
Контрольная работа
|
|
Дисциплина:
|
|
|
ВУЗ:
|
|
|
Город, год:
|
2020
|
|
Уникальность:
|
не определен % по системе Антиплагиат
|
Задание 1
Используя понятие доминирования решите графически матричную игру с нулевой суммой. Платежная матрица:
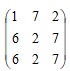
Задание 2
Сведите матричную игру к двойственной паре задач линейного программирования и решите её с помощью известных Вам методов математического программирования. Платежная матрица:
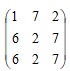
Задание 3
Найдите математическое ожидание выигрыша 1-ого игрока в матричной игре при использовании 1-ым игроком стратегии (1/2; 1/2; 0), а 2-ым игроком стратегии (1/3; 1/3; 1/3). Проверить с помощью Критерия оптимальности, являются ли эти стратегии оптимальными? Платёжная матрица:
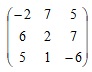
Задание 4
Игры с природой. Примите решения в условиях неопределённости с помощью правил Лапласа, Вальда, Сэвиджа и Гурвица (положить п=0,5). Матрица последствий:
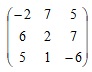 Задание 5
Задание 5Решите матричную игру с помощью итерационного алгоритма Брауна - Робинсон (провести 20 итераций). Сравнить это решение с решением 1 и 2 задач.
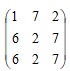 Задание 6
Задание 6Два независимых банка «А» и «В» планируют открыть филиалы для обслуживания населения в одном из трех городов К, L и М, расположенных вдоль автотрассы. Расстояния между любой парой соседних городов будем считать равными. Отношение клиентов в каждом городе к общему числу клиентов в этих городах таково: в городе К – 30%, L – 35%, М – 35%. Статистический анализ показал, что банк «А» обслуживает 70% клиентов в каждом городе, находящемся от его филиала на меньшем расстоянии, чем от филиала банка «В», 60% - в городах, лежащих на одном расстоянии и 50% - в городах, которые ближе к банку «В». Составить платежную матрицу для решения матричной игры с нулевой суммой. И решить матричную игру.
Задание 7
Придумать свою биматричную экономическую задачу и решить ее в некооперативном и кооперативном вариантах.
|
КУПИТЬ РАБОТУ
|
| СТОИМОСТЬ РАБОТЫ:
|
950 руб.
|
| - Введите нужную сумму и нажмите на кнопку "Перевести"
|
|
| - После оплаты отправьте СКРИНШОТ ОПЛАТЫ и ССЫЛКУ НА РАБОТУ на почту Studgold@mail.ru
|
|
| - После проверки платежа файл будет выслан на вашу почту в течение 48 ЧАСОВ.
|
|
| - Если цена работы не указана или менее 300 руб., то цену необоходимо уточнить в службе поддержки и только потом оплачивать.
|
|
| ПОДДЕРЖКА: |
Studgold@mail.ru
|

Минимальная длина комментария - 50 знаков. комментарии модерируются
|
СМОТРИТЕ ТАКЖЕ
|
Задачи по Теории игр. Решение 2-х задач (решение игр в смешанных стратегиях графическим методом и методами линейного программирования) [25-07-2021 15:19]
Задание 1 Решить в смешанных стратегиях графическим методом матричную игру, имеющую платежную матрицу: Задание 2 Решить матричную игру методами линейного программирования, если платежная матрица
Предмет: Теория игр
Шпаргалка по Теории игр [04-03-2015 08:41]
Экзаменационные вопросы по дисциплине «Теория игр» 1. Свойства седловых точек действительной функции двух векторных аргументов. 2. Критерий пессимизма-оптимизма Гурвица оптимальности чистых стратегий
Предмет: Теория игр
Лекции-шпаргалки по Теории игр с ответами на все вопросы [01-08-2018 22:25]
1. Задачи теории игр в экономике, финансах и бизнесе. 2. Основные понятия и определения теории антагонистических игр. 3. Чистые стратегии игроков. Выигрыш-функция и матрица выигрышей.
Предмет: Теория игр
Лабораторная работа по Теории Игр Вариант 3 [15-04-2013 15:59]
Задача. Предприятие может выпускать несколько видов продукции: A1, A2, A3, …, получая при этом прибыль. Величина прибыли определяется состоянием спроса («природой» рынка), который может находиться в
Предмет: Теория игр
Лабораторная работа по Теории Игр Вариант 1 [18-05-2013 15:51]
Постановка задачи Предприятие может выпускать несколько видов продукции А1, А2, А3, …, получая при этом прибыль. Величина прибыли определяется состоянием спроса ( «природой» рынка), который может
Предмет: Теория игр

