Задачи по Линейной алгебре с решением
|
ИНФОРМАЦИЯ
|
|
|
Вид работы:
|
Задачи
|
|
Дисциплина:
|
|
|
ВУЗ:
|
|
|
Город, год:
|
Город не указан 2015
|
|
Уникальность:
|
% по системе
|
Задача 54. Известны длины векторов a и b; α – угол между этими векторами.
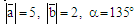
1) Вычислить:
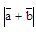 и
и 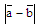
2) 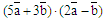
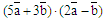
3) Найти площадь треугольника, построенного на векторах
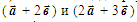
4) Сделать чертеж.
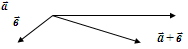
Задача 34.
Известны координаты трех вершин А, В, D параллелограмма АВСD. Средствами векторной алгебры требуется найти:
1. Координаты точки С – четвертой вершины параллелограмма;
2. Найти проекции вектора АВ на вектор AD и вектора АD на вектор АВ;
3. Найти угол между диагоналями параллелограмма;
4. Найти площадь параллелограмма;
5. Найти объем пирамиды, основанием которой является ∆АВС, а вершина расположена в начале координат.
А ( 3; -7; 0 ), В ( -9; -8; -5 ), D ( 0; -3; 4 )
Задача 54. Даны матрицы:
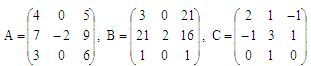
Вычислить: ( В - 2А ) • С
Задача 74. Решите систему линейных уравнений:
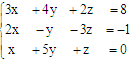
1. методом Крамера;
2. матричным методом;
3. методом Гаусса.
Аналитическая геометрия
Задача 94. Даны координаты вершин треугольника АВС. Найти:
1) длину стороны АВ;
2) уравнения сторон АВ и ВС и их угловые коэффициенты;
3) угол В в радианах с точностью до двух знаков;
4) уравнение высоты СD и ее длину;
5) уравнение медианы АЕ и координаты точки К пересечения этой медианы с высотой СD;
6) уравнение прямой, проходящей через точку К параллельно стороне АВ;
7) сделать чертеж А (-4; 10), В (8; 1), С (12; 23).
Задача 94. Даны вершины А(-3;-2), В(4;-1), С(1; 3) трапеции АВСD (AD || ВC). Известно, что диагонали трапеции взаимно перпендикулярны. Найти координаты вершины D этой трапеции. Сделать чертеж.
|
КУПИТЬ РАБОТУ
|
| СТОИМОСТЬ РАБОТЫ:
|
|
| - Введите нужную сумму и нажмите на кнопку "Перевести"
|
|
| - После оплаты отправьте СКРИНШОТ ОПЛАТЫ и ССЫЛКУ НА РАБОТУ на почту Studgold@mail.ru
|
|
| - После проверки платежа файл будет выслан на вашу почту в течение 48 ЧАСОВ.
|
|
| - Если цена работы не указана или менее 300 руб., то цену необоходимо уточнить в службе поддержки и только потом оплачивать.
|
|
| ПОДДЕРЖКА: |
Studgold@mail.ru
|

Минимальная длина комментария - 50 знаков. комментарии модерируются
|
СМОТРИТЕ ТАКЖЕ
|
Контрольная работа по Линейной алгебре Вариант 5 [08-12-2015 01:02]
1. Дана матрица Найти ранг матрицы 2. По формулам Крамера решить систему: 3. Определить, имеет ли однородная система ненулевое решение. Найти общее решение
Предмет: Математический анализ и линейная алгебра
Контрольная работа по Линейной алгебре Вариант 1 [03-05-2015 14:21]
1. Найти собственные векторы и собственные значения матрицы: 2. Относительно базиса заданы векторы а) доказать, что векторы образуют базис пространства
Предмет: Математический анализ и линейная алгебра
Контрольная работа по Линейной алгебре Вариант 2 [11-02-2015 22:18]
Задача 1. Даны матрицы: Найти ранг матрицы C=A*В Задача 2. Методом обратной матрицы решить систему: Задача 3. Определить, имеет ли однородная система: ненулевое решение. Найти общее
Предмет: Математический анализ и линейная алгебра
Контрольная работа №1 по Математическому анализу и линейной алгебре Вариант 10 [10-08-2012 13:34]
Внимание! У Вас нет прав для просмотра скрытого текста.
Предмет: Математический анализ и линейная алгебра
Контрольная работа по Линейной алгебре Вариант 1 [11-04-2016 02:46]
Контрольная работа № 1 по Линейной алгебре Вариант №1, 1 курс, заочное отделение 1. Даны матрицы Найти ранг матрицы C=A-1∙B. 2. По формулам Крамера решить систему:
Предмет: Математический анализ и линейная алгебра
Контрольная работа по Линейной алгебре №1 и №2 Вариант 7 [02-02-2015 17:30]
Контрольная работа №1 1. Даны матрицы Найти ранг матрицы С = А·В. 2. Методом обратной матрицы решить систему: 3. Установить, имеет ли однородная система ненулевое решение. Найти
Предмет: Математический анализ и линейная алгебра

