Контрольная работа по Линейной алгебре №1 и №2 Вариант 7
|
ИНФОРМАЦИЯ
|
|
|
Вид работы:
|
Контрольная работа
|
|
Дисциплина:
|
|
|
ВУЗ:
|
|
|
Город, год:
|
Город не указан 2015
|
|
Уникальность:
|
% по системе
|
1. Даны матрицы
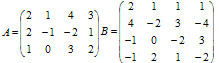
2. Методом обратной матрицы решить систему:
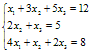
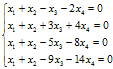
4. Найти значение параметра α, при котором векторы и перпендикулярны, если
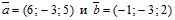
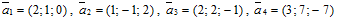
в некотором базисе. Показать, что векторы , , образуют базис, и найти координаты вектора в этом базисе.
6. Найти собственные значения и собственные векторы линейного оператора А, заданного матрицей 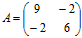
7. а) Методом Лагранжа привести квадратичную форму
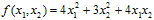
б) По критерию Сильвестра исследовать на знакоопределенность квадратичную форму
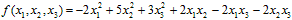
1. Точки А(-3; -2), В(0; -1) и С(2; 5) являются вершинами треугольника АВС. Определить координаты точки Н – основания медианы АН треугольника АВС и составить уравнение медианы треугольника, опущенной из точки А на сторону ВС. Сделать чертеж.
2. Составить уравнение гиперболы, фокусыкоторой лежат на оси абсцисс, симметрично относительно начала координат, если
уравнение ее асимптот , а расстояние между вершинами равно 48.
3. Составить уравнение диаметраокружности , перпендикулярного к прямой 5x + 2y – 13 = 0.
4. Написать уравнение плоскости,проходящей через точку М(2; -1; 4) и линию пересечения плоскостей 2x + 3y – z = 2 и х = 1.
5. Верно ли, что прямая параллельна плоскости 2x + y – 2z = 9? Если да, то найти расстояние между этими прямой и плоскостью.
|
КУПИТЬ РАБОТУ
|
| СТОИМОСТЬ РАБОТЫ:
|
|
| - Введите нужную сумму и нажмите на кнопку "Перевести"
|
|
| - После оплаты отправьте СКРИНШОТ ОПЛАТЫ и ССЫЛКУ НА РАБОТУ на почту Studgold@mail.ru
|
|
| - После проверки платежа файл будет выслан на вашу почту в течение 48 ЧАСОВ.
|
|
| - Если цена работы не указана или менее 300 руб., то цену необоходимо уточнить в службе поддержки и только потом оплачивать.
|
|
| ПОДДЕРЖКА: |
Studgold@mail.ru
|

Минимальная длина комментария - 50 знаков. комментарии модерируются
|
СМОТРИТЕ ТАКЖЕ
|
Контрольная работа по Линейной алгебре Вариант 2 [11-02-2015 22:18]
Задача 1. Даны матрицы: Найти ранг матрицы C=A*В Задача 2. Методом обратной матрицы решить систему: Задача 3. Определить, имеет ли однородная система: ненулевое решение. Найти общее
Предмет: Математический анализ и линейная алгебра
Контрольная работа по Линейной алгебре №1 Вариант 9 [22-01-2015 17:57]
1. Даны матрицы Определить, имеет ли матрица С = А*В обратную. 2. Решить систему линейных уравнение пол формулам Крамера: 3. Решить систему линейных уравнений. Найти какое-нибудь
Предмет: Математический анализ и линейная алгебра
Контрольная работа по Линейной алгебре Вариант 5 [08-12-2015 01:02]
1. Дана матрица Найти ранг матрицы 2. По формулам Крамера решить систему: 3. Определить, имеет ли однородная система ненулевое решение. Найти общее решение
Предмет: Математический анализ и линейная алгебра
Контрольная работа по Линейной алгебре Вариант 1 [19-02-2015 21:03]
Контрольная работа № 1 1. Даны матрицы 2. По формулам Крамера решить систему: 3. Решить систему линейных уравнений: 4. Найти длину вектора 5. Даны четыре вектора: в
Предмет: Математический анализ и линейная алгебра
Контрольная работа по Линейной алгебре Вариант 1 [11-04-2016 02:46]
Контрольная работа № 1 по Линейной алгебре Вариант №1, 1 курс, заочное отделение 1. Даны матрицы Найти ранг матрицы C=A-1∙B. 2. По формулам Крамера решить систему:
Предмет: Математический анализ и линейная алгебра
Контрольная работа по Линейной алгебре Вариант 1 [03-05-2015 14:21]
1. Найти собственные векторы и собственные значения матрицы: 2. Относительно базиса заданы векторы а) доказать, что векторы образуют базис пространства
Предмет: Математический анализ и линейная алгебра

