Векторная алгебра и аналитическая геометрия Контрольная работа Вариант 22
|
ИНФОРМАЦИЯ
|
|
|
Вид работы:
|
Контрольная работа
|
|
Дисциплина:
|
|
|
ВУЗ:
|
|
|
Город, год:
|
Красноярск 2015
|
|
Уникальность:
|
% по системе
|
1. Перемножить матрицы:
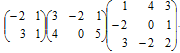
2. Вычислить определители:
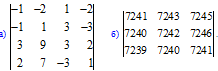
3. Решить систему линейных уравнений: а) методом Крамера, б) при помощи обратной матрицы, в) методом Гаусса.
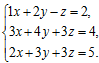
4. Найти общее решение методом Гаусса
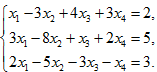
частное решение
5. Вычислить ранг матрицы: а) методом окаймляющих миноров; б) методом элементарных преобразований:
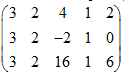
6. Показать, что векторы a, b, c, образуют базис. Найти разложение вектора d по этому базису, если a = (2;4;2), b = (–1;–2;–2), c = (3;5;1), d = (3;5;–1).
7. Вычислить выражения, используя определения и свойства скалярного и векторного произведений:
а) (a–3b)(2a+b), б) |(a–3b)x(2a+b)|,
где |a|=4, |b|=2, a^b=2п/3.
8. Даны координаты вершин пирамиды ABCD. Найти: а) объем пирамиды, б) площадь грани ABC, в) косинус угла между ребрами AB и AC, г) уравнение прямой АВ, д) уравнение плоскости АВС, если A(1;3;–1), B(2;–2;0), C(–1;1;2), D(3;2;1).
Даны координаты вершин пирамиды А1,А2,А3,А4
Определим координаты векторов с вершинами в данных точках.
9. Составить каноническое уравнение прямой:
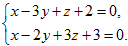

11. Вывести уравнение кривой, если абсолютная величина разности расстояний от каждой ее точки до точек F1(–7;0) и F2(13;0) есть величина постоянная и равна p=16. Сделать чертеж.
12. Привести уравнение 36x2+49y2+72x–196y–1442=0 к каноническому виду, определить тип кривой и сделать чертеж.
|
КУПИТЬ РАБОТУ
|
| СТОИМОСТЬ РАБОТЫ:
|
не помню руб.
|
| - Введите нужную сумму и нажмите на кнопку "Перевести"
|
|
| - После оплаты отправьте СКРИНШОТ ОПЛАТЫ и ССЫЛКУ НА РАБОТУ на почту Studgold@mail.ru
|
|
| - После проверки платежа файл будет выслан на вашу почту в течение 48 ЧАСОВ.
|
|
| - Если цена работы не указана или менее 300 руб., то цену необоходимо уточнить в службе поддержки и только потом оплачивать.
|
|
| ПОДДЕРЖКА: |
Studgold@mail.ru
|

Минимальная длина комментария - 50 знаков. комментарии модерируются
|
СМОТРИТЕ ТАКЖЕ
|
Задачи по Аналитической геометрии (3 решенные задачи) [23-12-2015 11:18]
531. Даны две плоскости , . С помощью рангов r и R матриц выразить условия, необходимые и достаточные для того, чтобы плоскости: 1) пересекались;
Предмет: Геометрия

